Quantum theorists at UBC’s Blusson Quantum Matter Institute have proposed a new approach to studying stacking ferroelectricity—spontaneous electric polarization—in layered, two-dimensional lab-grown materials.
Ferroelectric materials are unique in their ability to “remember” their new state after the electric field is removed, which makes them useful in applications including solar cell technology and compact memory devices.

Image: Dr. Benjamin Zhou, Postdoctoral Fellow.
“We’ve been learning in recent years that quantum geometry underlies a surprising range of the observable properties of materials,” said Dr. Marcel Franz, deputy scientific director at UBC Blusson QMI and a professor with the Department of Physics & Astronomy. “This work adds an important new entry to the growing list of phenomena that can be elucidated using this fascinating geometric approach.”
Ferroelectricity is a property that allows materials to have a built-in electric polarization. Ferroelectric materials have switchable polarization that can be controlled by an electric field, while stacking ferroelectrics are formed by assembling two atomically thin non-polar layers that create polarization through their special way of stacking.
“The most exciting part of our discovery is that the underlying physics behind stacking ferroelectricity can, in fact, be understood as a geometric property,” said UBC Blusson QMI postdoctoral fellow Dr. Benjamin Zhou, lead author of the study published in the journal Physical Review Letters.
“To establish the meaningful connection between stacking ferroelectricity and geometry, we had to go through detailed model analysis and rigorous numerical calculations for different types of ferroelectric materials such as honeycomb bilayers, rhombohedral bilayer molybdenum disulfide (3R-MoS2) and bilayer tungsten ditelluride (WTe2),” Dr. Zhou said. “The results confirm that our geometric approach works well for all these materials.”
Until now, scientists have studied stacking ferroelectric materials in two ways: symmetry analysis, which determines if the material can be polar, and computational approaches that provide the magnitude of the polarization. However, these methods are limited in describing the robustness of the polarization.
The new quantum-geometric approach allows the researchers to look at the polarization properties as a geometric feature of the model, which they describe using a visual representation of a vector moving over a sphere.
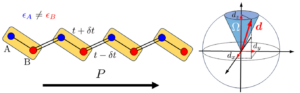
Left: Schematic of a one-dimensional chain known as the Su-Schrieffer-Heeger (SSH) chain. The model for such a chain can be described by a vector d. The study by QMI theorists reveals that the quantum-geometric property of stacking ferroelectrics mimics that of the SSH chain. Right: Vector d travels along some trajectory over the sphere, which provides useful information on the robustness of electric polarization.
“For each stacking ferroelectric material, the trajectory of its corresponding unit vector across the sphere is unique, allowing us to easily identify how robust the polarization can be and predict what types of materials can exhibit strong polarity,” said Dr. Zhou. “This discovery provides us with a new powerful lens to look into the underlying physics of ferroelectrics.”
The study was inspired by the previous experimental work led by Blusson QMI investigator Dr. Ziliang Ye, published in nature photonics, where Zhou and Franz contributed to the theoretical explanation. The results demonstrated by Ye’s group in 2022 were among the first experiments in the world to achieve ferroelectric spontaneous polarization via a designed stacking order between atomic layers.
“The modern theory of polarization explains bulk ferroelectrics using the Berry phase concept which becomes tricky to deal with for stacking ferroelectrics in the 2D limit. Our geometric approach reconnects the origin of polarization in 2D ferroelectrics with the Berry phase concept,” said Vedangi Pathak, a PhD student in Franz’s group who co-authored the study. “Our work provides a very simple framework that anyone with a physics background can use in their research.”


